P10511 题解

本文距离上次更新已过去 0 天，部分内容可能已经过时，请注意甄别。

思路

首先好像高一就学过 。但还是推一下：
令 ，则

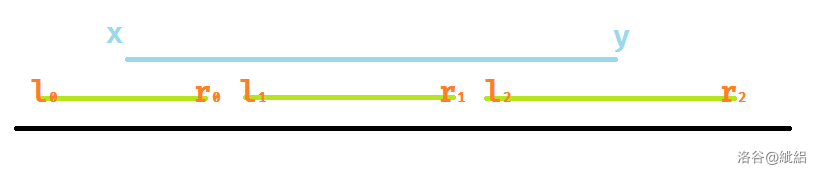
也就是要维护区间平方和与区间和。这可以考虑用前缀和维护。考虑到有散块的可能，所以先把夹在 和 中间的整块求出来，再把 旁边的或 旁边的散块求出来。记得及时取膜。

我们可以先把 和 所在的块的坐标求出来，再把指针各往中间移一块来计算整块。

例如，想要求 所在的块编号，只要找到离它最近且大于等于它的 或小于它 即可。注意， 可以和 重合，但 不可以，如果重合的话 号块也可以算作被夹在中间的块了。代码写出来就是 dx = lower_bound(r + 1, r + m + 1, x) - r; 或 dx = lower_bound(l + 1, l + m + 1, x) - l - 1。 所在的编号也是差不多的求法。

其他小细节在代码注释里。注意取膜哦！

代码

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

const ll M = 2e5 + 100, mod = 998244353;
ll n, m, q;
ll l[M], r[M];
ll s[M], qs[M], len[M], b[M];

int main()
{
    cin >> n >> m >> q;
    for (int i = 1; i <= m; i++)
    {
        cin >> l[i] >> r[i] >> b[i]; b[i] %= mod;
        len[i] = (r[i] - l[i] + 1) % mod;  
        s[i] = (len[i] * b[i]) % mod; 
        qs[i] = (s[i] * b[i]) % mod; 
        len[i] = (len[i - 1] + len[i]) % mod;
        s[i] = (s[i - 1] + s[i]) % mod;
        qs[i] = (qs[i - 1] + qs[i]) % mod;
    }
    
    for (int i = 1; i <= q; i++)
    {
        /* 一开始想先把离 x/y 右/左 边最近的 左/右 端点编号求出来的……但是实现起来有点麻烦（ */
        
        ll x, y, dx, dy /* dx 为 x 所在的编号；dy 含义亦然 */, S, QS, ans; cin >> x >> y;
        dx = lower_bound(l + 1, l + m + 1, x) - l - 1, // 也就是 dx = lower_bound(r + 1, r + m + 1, x) - r;
        dy = lower_bound(r + 1, r + m + 1, y) - r;
        if (dx == dy) { cout << 0 << endl; continue; }
        
//      S = S + (r[dx] - x + 1) * b[dx] + (y - l[dy] + 1) * b[dy];  
        S = (r[dx] - x + 1) % mod * b[dx] % mod + (y - l[dy] + 1) % mod * b[dy] % mod;
        QS = (r[dx] - x + 1) % mod * b[dx] % mod * b[dx] % mod + (y - l[dy] + 1) % mod* b[dy] % mod * b[dy] % mod;
    
        dx++, dy--; // 移到里面夹着的整块
        if (dx <= dy) // 排除里面没夹着整块的情况
        {
            S = (S + s[dy] - s[dx - 1] + mod) % mod;
            QS = (QS + qs[dy] - qs[dx - 1] + mod) % mod;
        }
        ans = ((y - x + 1) % mod * QS % mod - S * S % mod + mod) % mod;
        cout << (ans + mod) % mod << endl;
    }
    
    return 0;
}